Рішення системи рівнянь в Microsoft Excel

Уміння вирішувати системи рівнянь часто може принести користь не тільки в навчанні, а й на практиці. У той же час, далеко не кожен користувач ПК знає, що в Ексель існує власні варіанти рішень лінійних рівнянь. Давайте дізнаємося, як із застосуванням інструментарію цього табличного процесора виконати це завдання різними способами.

варіанти рішень

Будь-яке рівняння може вважатися вирішеним тільки тоді, коли будуть знайдені його коріння. У програмі Excel існує кілька варіантів пошуку коренів. Давайте розглянемо кожен з них.

Спосіб 1: матричний метод

Найпоширеніший спосіб вирішення системи лінійних рівнянь інструментами Excel - це застосування матричного методу. Він полягає в побудові матриці з коефіцієнтів виразів, а потім у створенні оберненої матриці. Спробуємо використовувати даний метод для вирішення наступної системи рівнянь:


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


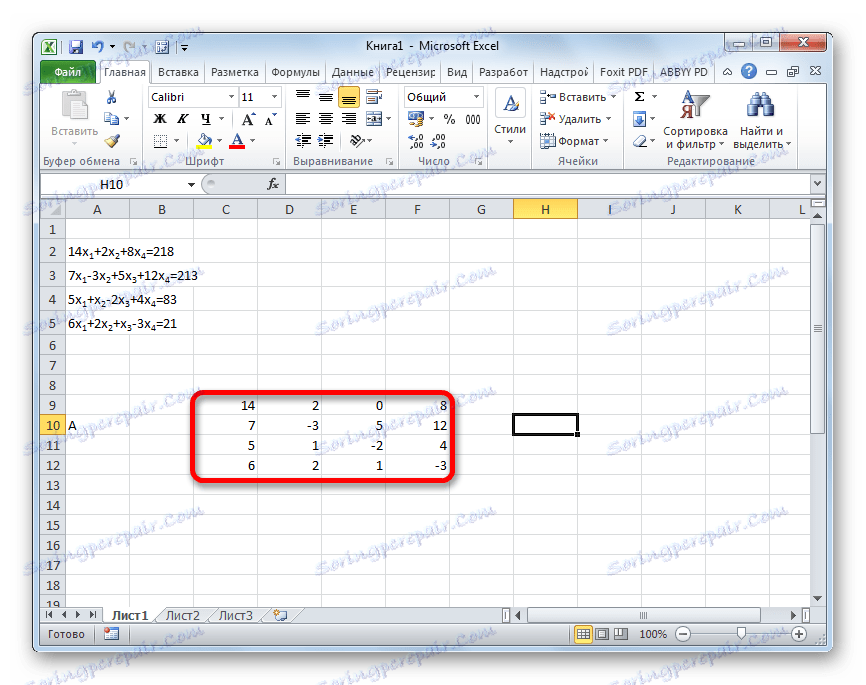
1. Заповнюємо матрицю числами, які є коефіцієнтами рівняння. Дані числа повинні розташовуватися послідовно по порядку з урахуванням розташування кожного кореня, з яким вони відповідають. Якщо в якомусь виразі один з коренів відсутня, то в цьому випадку коефіцієнт вважається рівним нулю. Якщо коефіцієнт не позначений в рівнянні, але відповідний корінь є, то вважається, що коефіцієнт дорівнює 1. Позначаємо отриману таблицю, як вектор A.
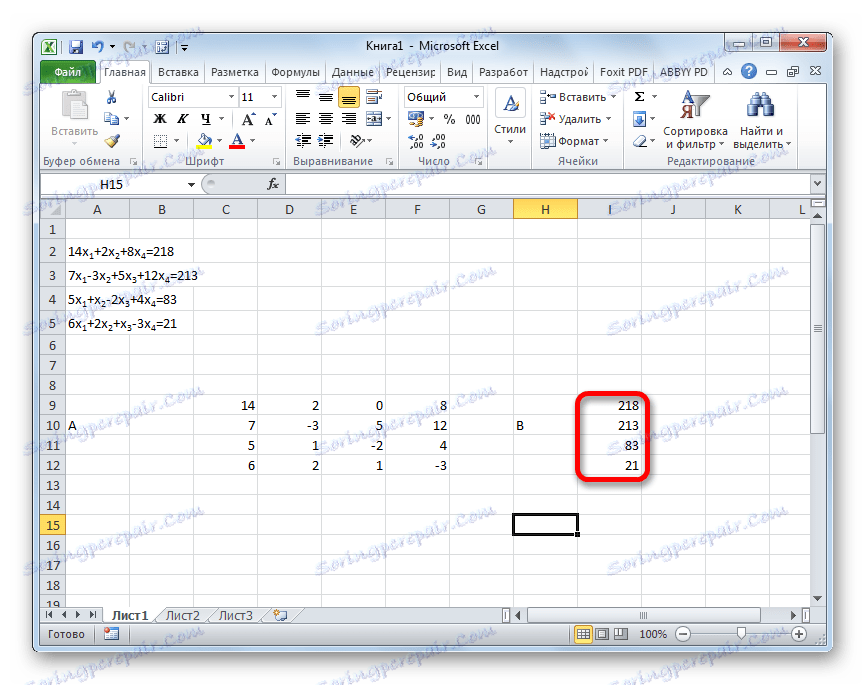
2. Окремо записуємо значення після знака «дорівнює». Позначаємо їх загальним найменуванням, як вектор B.
3. Тепер для знаходження коренів рівняння, перш за все, нам потрібно відшукати матрицю, зворотну існуючої. На щастя, в Ексель є спеціальний оператор, який призначений для вирішення даного завдання. Називається він МОБР. Він має досить простий синтаксис:

   =МОБР(массив)

   Аргумент «Масив» - це, власне, адреса вихідної таблиці.

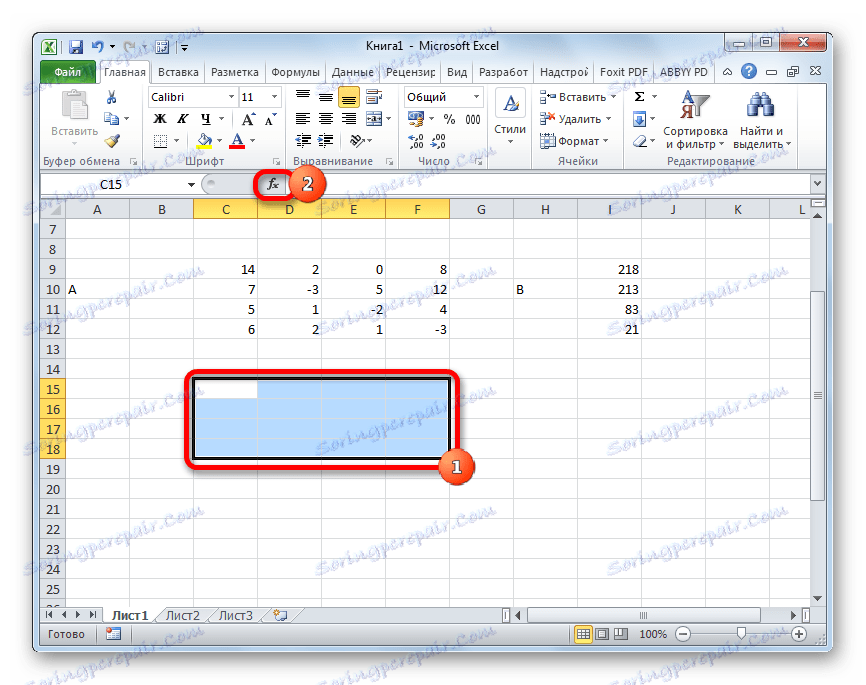
   Отже, виділяємо на аркуші область порожніх клітинок, яка за розміром дорівнює діапазону вихідної матриці. Клацаємо по кнопці «Вставити функцію», розташовану біля рядка формул.

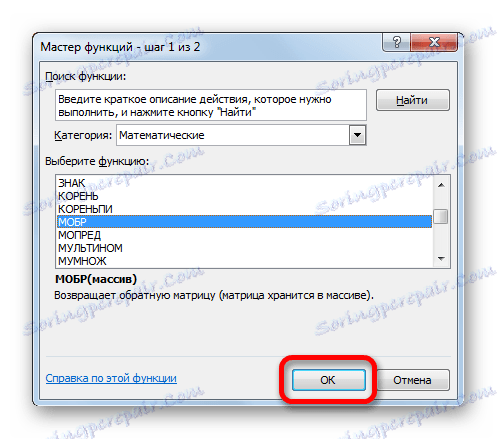
4. Виконується запуск Майстра функцій. Переходимо в категорію «Математичні». У представився списку шукаємо найменування «МОБР». Після того, як воно знайдено, виділяємо його і тиснемо на кнопку «OK».
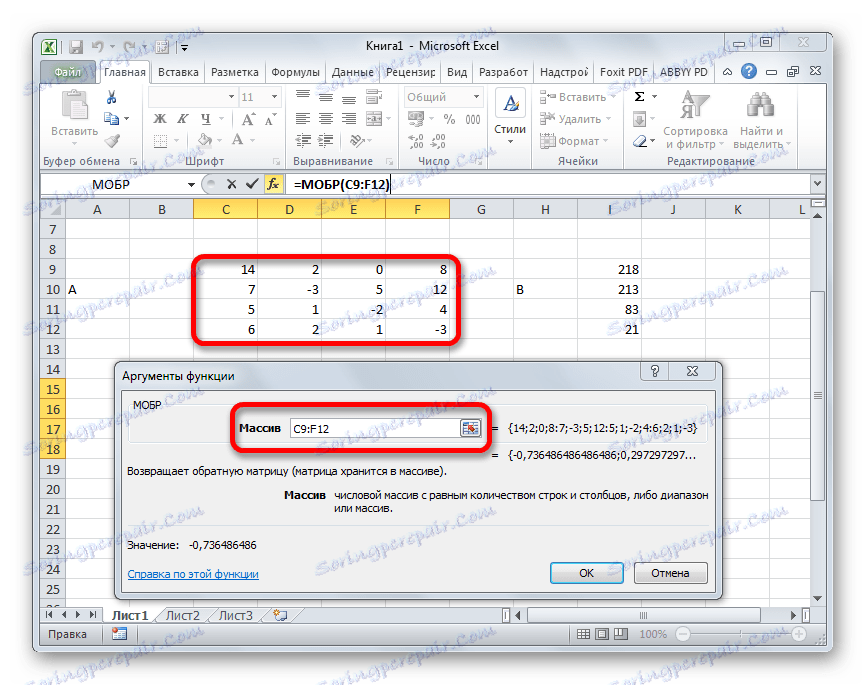
5. Запускається вікно аргументів функції МОБР. Воно по числу аргументів має всього одне поле - «Масив». Тут потрібно вказати адресу нашої таблиці. Для цих цілей встановлюємо курсор в це поле. Потім затискаємо ліву кнопку миші і виділяємо область на аркуші, в якій знаходиться матриця. Як бачимо, дані про координати розміщення автоматично заносяться в поле вікна. Після того, як ця задача виконана, найбільш очевидним було б натиснути на кнопку «OK», але не варто поспішати. Справа в тому, що натискання на цю кнопку є рівнозначним застосуванню команди Enter. Але при роботі з масивами після завершення введення формули слід не клікати по кнопці Enter, а зробити набір клавіш Ctrl + Shift + Enter. Виконуємо цю операцію.
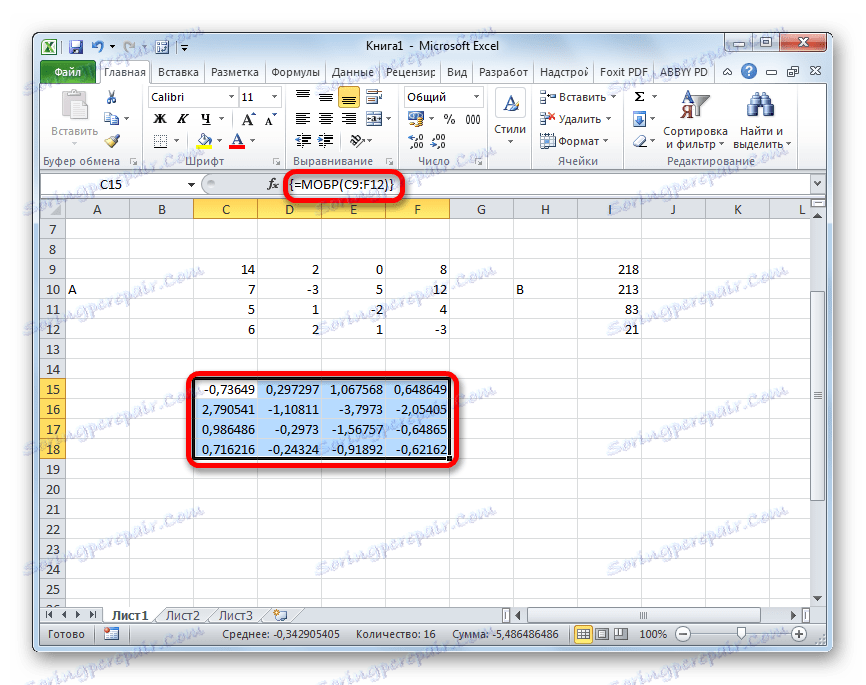
6. Отже, після цього програма робить обчислення і на виході в попередньо виділеної області ми маємо матрицю, зворотну даної.
7. Тепер нам потрібно буде помножити зворотну матрицю на матрицю B, яка складається з одного стовпця значень, розташованих після знака «дорівнює» у виразах. Для множення таблиць в Ексель також є окрема функція, яка називається МУМНОЖ. Даний оператор має наступний синтаксис:

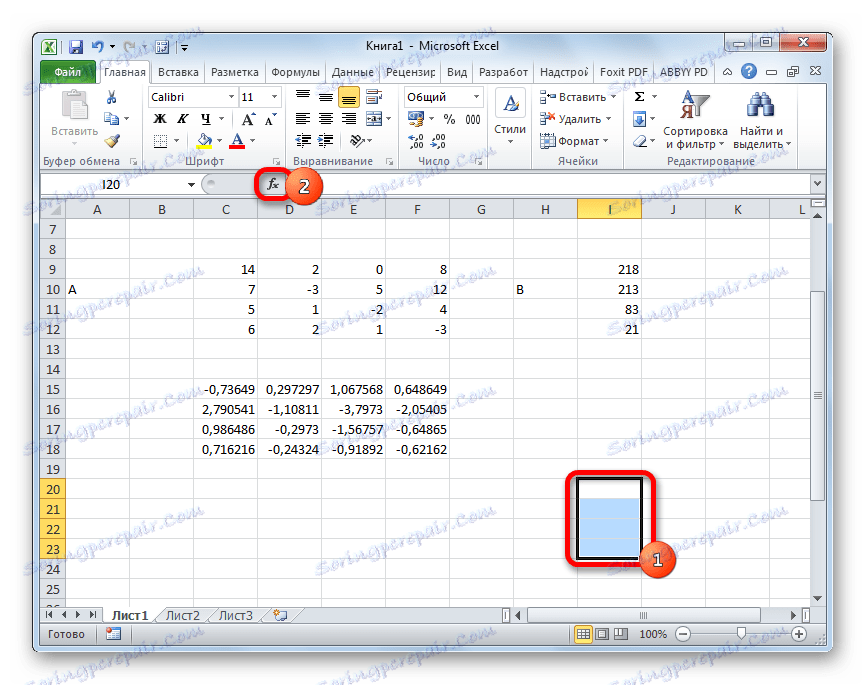
   =МУМНОЖ(Массив1;Массив2)

   Виділяємо діапазон, в нашому випадку складається з чотирьох осередків. Далі знову запускаємо Майстер функцій, натиснувши значок «Вставити функцію».

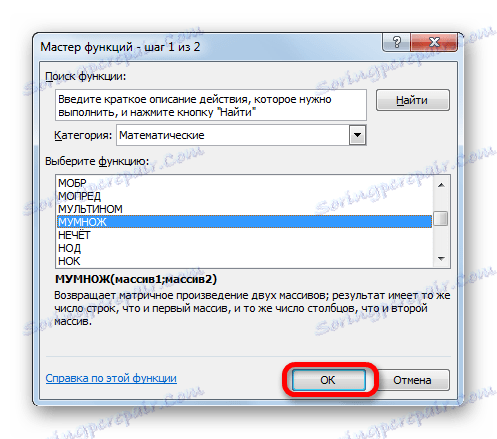
8. У категорії «Математичні», запуститься Майстра функцій, виділяємо найменування «МУМНОЖ» і тиснемо на кнопку «OK».
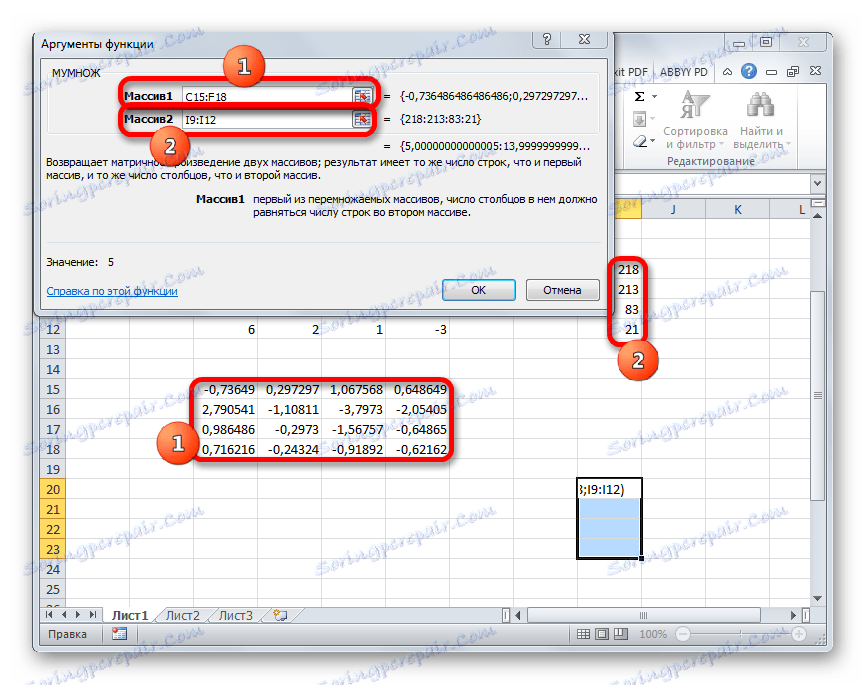
9. Активується вікно аргументів функції МУМНОЖ. В поле «массів1» заносимо координати нашої оберненої матриці. Для цього, як і в минулий раз, встановлюємо курсор в поле і з затиснутою лівою кнопкою миші виділяємо курсором відповідну таблицю. Аналогічну дію проводимо для внесення координат в поле «массів2», тільки на цей раз виділяємо значення колонки B. Після того, як вищевказані дії проведені, знову не поспішаємо тиснути на кнопку «OK» або клавішу Enter, а набираємо комбінацію клавіш Ctrl + Shift + Enter.
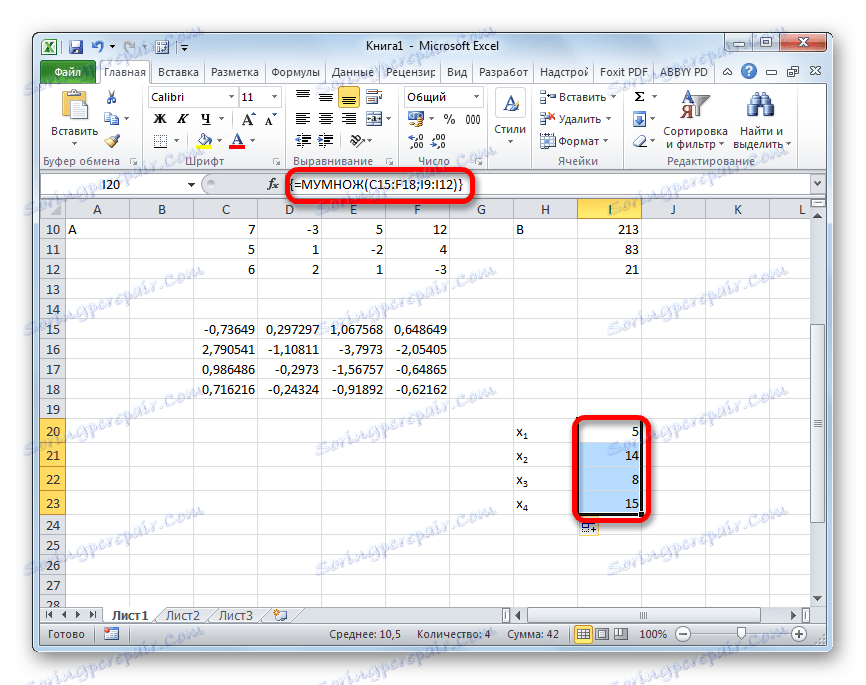
10. Після цієї події в попередньо виділеної осередку відобразяться коріння рівняння: X1, X2, X3 і X4. Вони будуть розташовані послідовно. Таким чином, можна сказати, що ми вирішили цю систему. Для того, щоб перевірити правильність рішення досить підставити в вихідну систему виразів дані відповіді замість відповідних коренів. Якщо рівність буде дотримано, то це означає, що представлена ​​система рівнянь вирішена вірно.

урок: Зворотній матриця в Excel

Спосіб 2: підбір параметрів

Другий відомий спосіб вирішення системи рівнянь в Ексель - це застосування методу підбору параметрів. Суть даного методу полягає в пошуку від зворотного. Тобто, грунтуючись на відомому результаті, ми проводимо пошук невідомого аргументу. Давайте для прикладу використовуємо квадратне рівняння

3x^2+4x-132=0

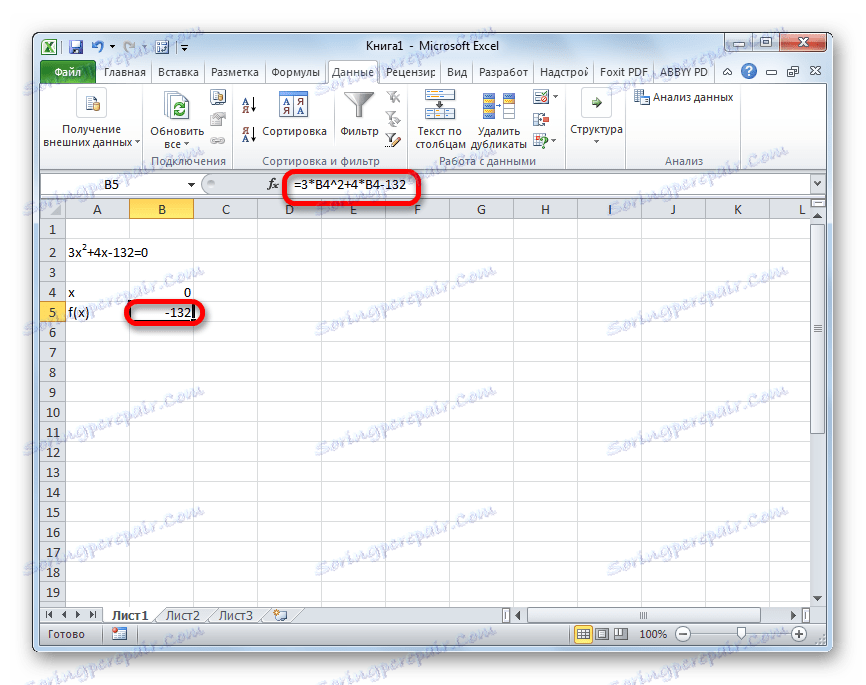
1. Приймаємо значення x за рівне 0. Вираховуємо відповідне для нього значення f (x), застосувавши таку формулу:

   =3*x^2+4*x-132

   Замість значення «X» підставляємо адресу тієї комірки, де розташоване число 0, прийняте нами за x.

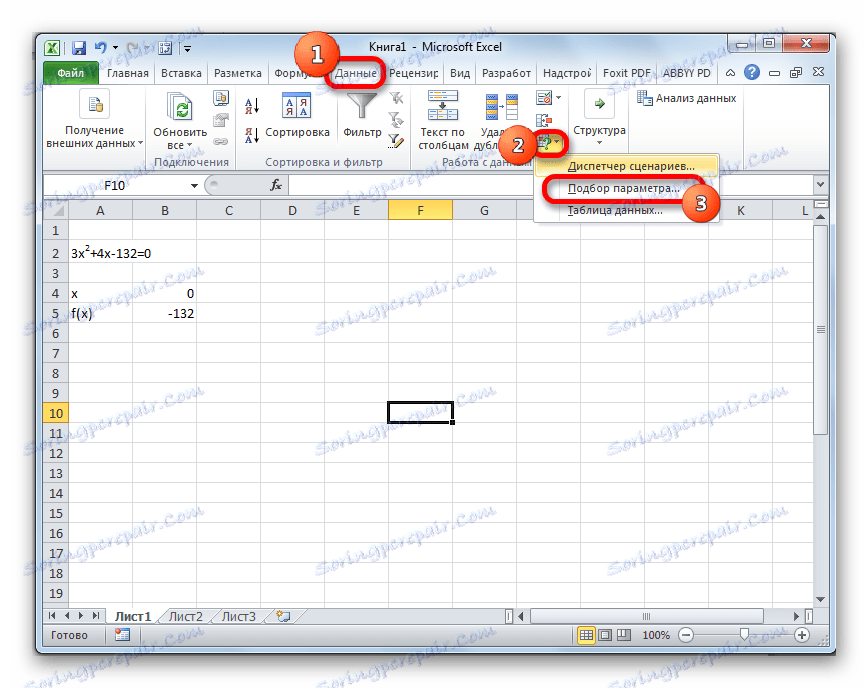
2. Переходимо у вкладку «Дані». Тиснемо на кнопку «Аналіз« що якщо »». Ця кнопка розміщена на стрічці в блоці інструментів «Робота з даними». Відкривається список, що випадає. Вибираємо в ньому позицію «Підбір параметра ...».
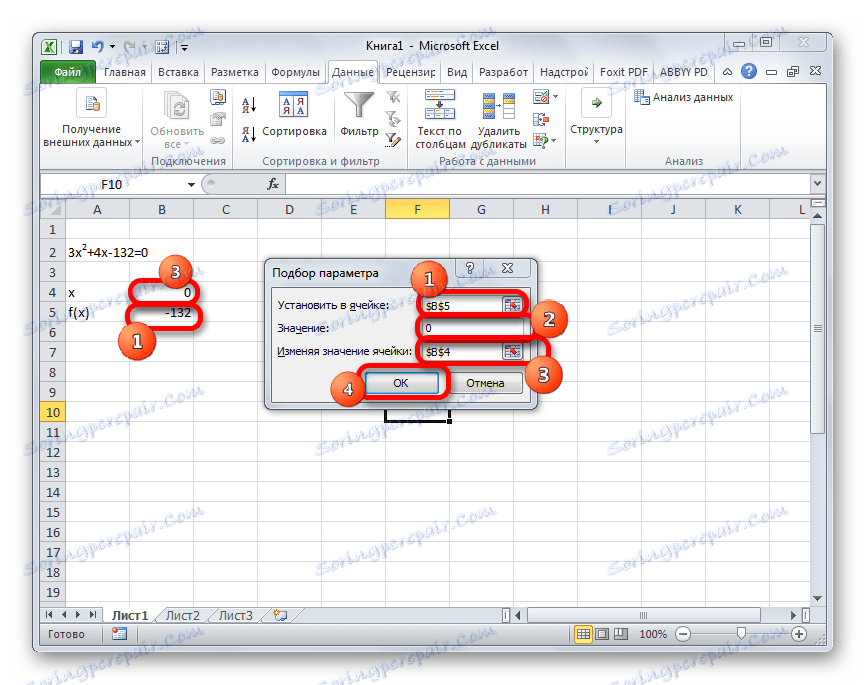
3. Запускається вікно підбору параметрів. Як бачимо, воно складається з трьох полів. В поле «Встановити в осередку» вказуємо адресу осередки, в якій знаходиться формула f (x), розрахована нами трохи раніше. В поле «Значення» вводимо число «0». В поле «Змінюючи значення» вказуємо адресу осередки, в якій розташоване значення x, раніше прийняте нами за 0. Після виконання даних дій тиснемо на кнопку «OK».
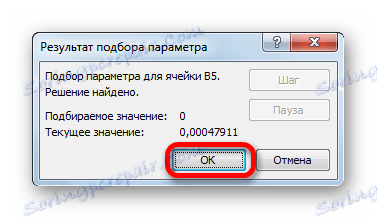
4. Після цього Ексель зробить обчислення за допомогою підбору параметра. Про це повідомить з'явилося інформаційне вікно. У ньому слід натиснути на кнопку «OK».
5. Результат обчислення кореня рівняння буде знаходитися в тій комірці, яку ми призначили в поле «Змінюючи значення». У нашому випадку, як бачимо, x буде дорівнює 6.

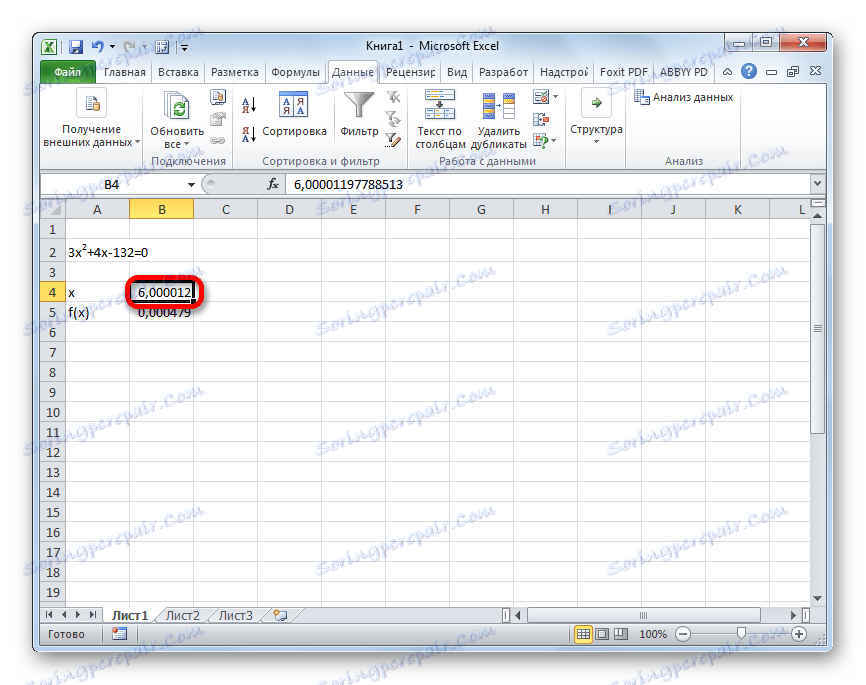
Цей результат також можна перевірити, підставивши це значення в вирішувалася вираз замість значення x.

урок: Підбір параметра в Excel

Спосіб 3: метод Крамера

Тепер спробуємо вирішити систему рівнянь методом Крамера. Для прикладу візьмемо все ту ж систему, яку використовували в Способі 1:


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21


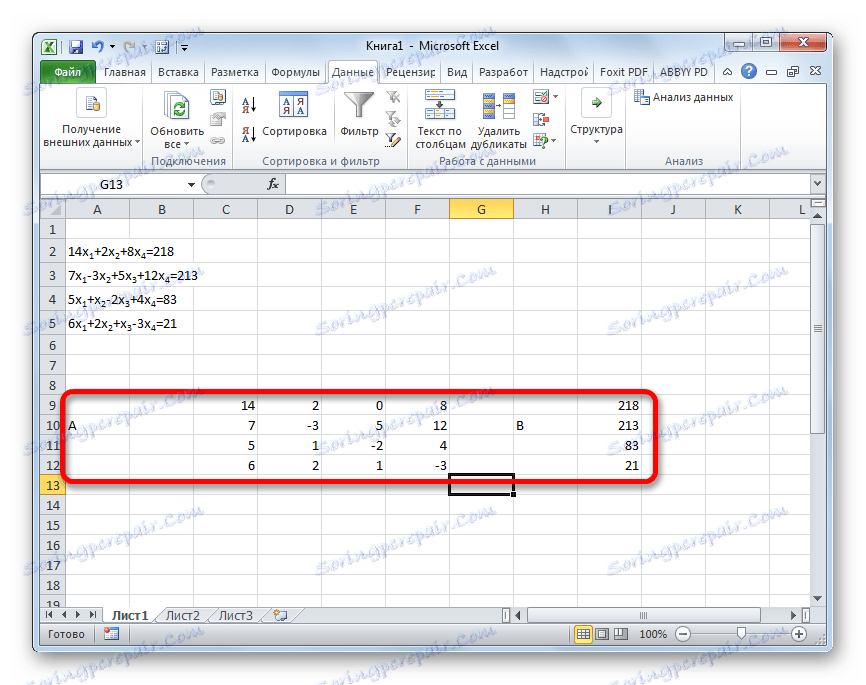
1. Як і в першому способі, складаємо матрицю A з коефіцієнтів рівнянь і таблицю B зі значень, які стоять після знака «дорівнює».
2. Далі робимо ще чотири таблиці. Кожна з них є копією матриці A, тільки у цих копій по черзі один стовпець замінений на таблицю B. У першій таблиці - це перший стовпець, у другій таблиці - другий і т.д.
3. Тепер нам потрібно вирахувати визначники для всіх цих таблиць. Система рівнянь матиме рішення тільки в тому випадку, якщо всі визначники будуть мати значення, відмінне від нуля. Для розрахунку цього значення в Ексель знову є окрема функція - МОПРЕД. Синтаксис цього оператора наступний:

   =МОПРЕД(массив)

   Таким чином, як і у функції МОБР, єдиним аргументом виступає посилання на оброблювану таблицю.

   Отже, виділяємо клітинку, в якій буде виводитися визначник першої матриці. Потім тиснемо на знайому за попередніми способам кнопку «Вставити функцію».

4. Активується вікно Майстра функцій. Переходимо в категорію «Математичні» і серед списку операторів виділяємо там найменування «МОПРЕД». Після цього тиснемо на кнопку «OK».
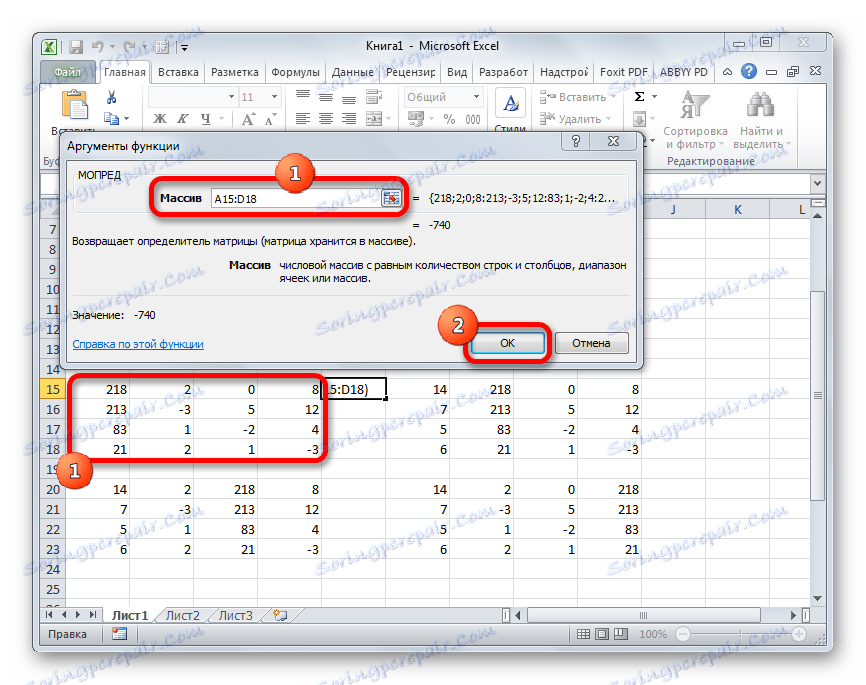
5. Запускається вікно аргументів функції МОПРЕД. Як бачимо, воно має тільки одне поле - «Масив». У це поле вписуємо адресу першої перетвореної матриці. Для цього встановлюємо курсор в поле, а потім виділяємо матричний діапазон. Після цього тиснемо на кнопку «OK». Ця функція виводить результат в одну клітинку, а не масивом, тому для отримання розрахунку не потрібно вдаватися до натискання комбінації клавіш Ctrl + Shift + Enter.
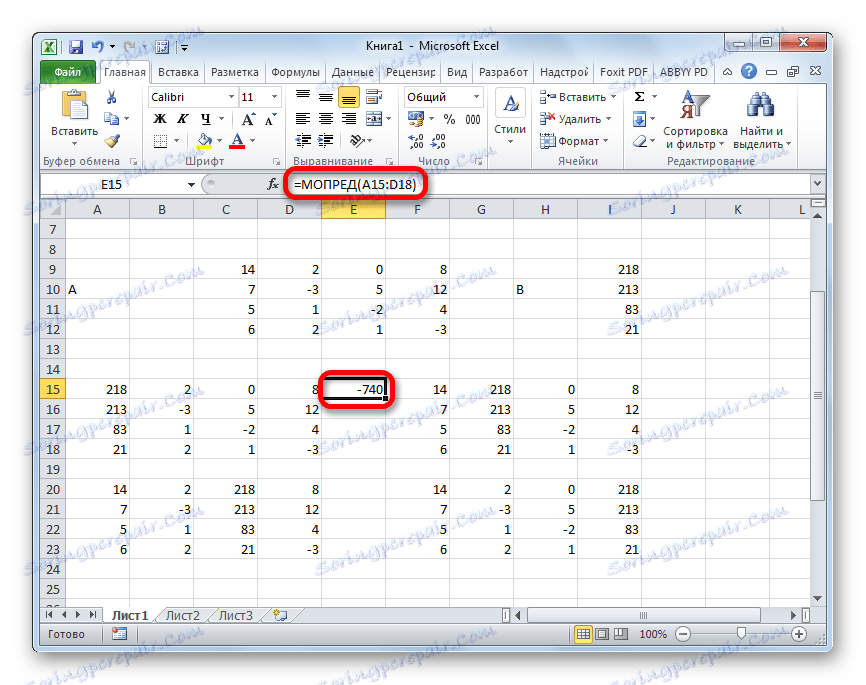
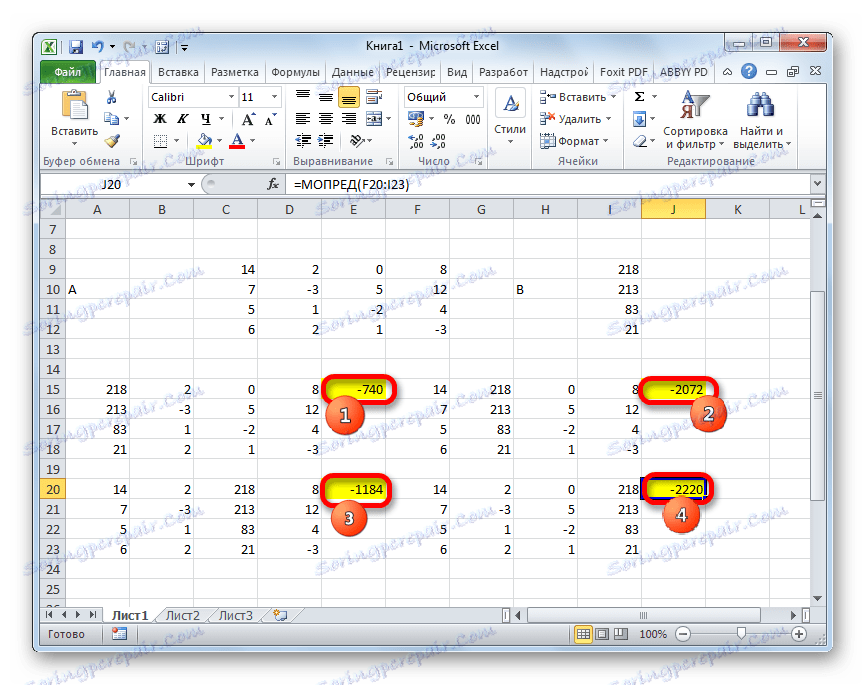
6. Функція виробляє підрахунок результату і виводить його в заздалегідь виділену клітинку. Як бачимо, в нашому випадку визначник дорівнює -740, тобто, не є рівним нулю, що нам підходить.
7. Аналогічним чином виробляємо підрахунок визначників для інших трьох таблиць.
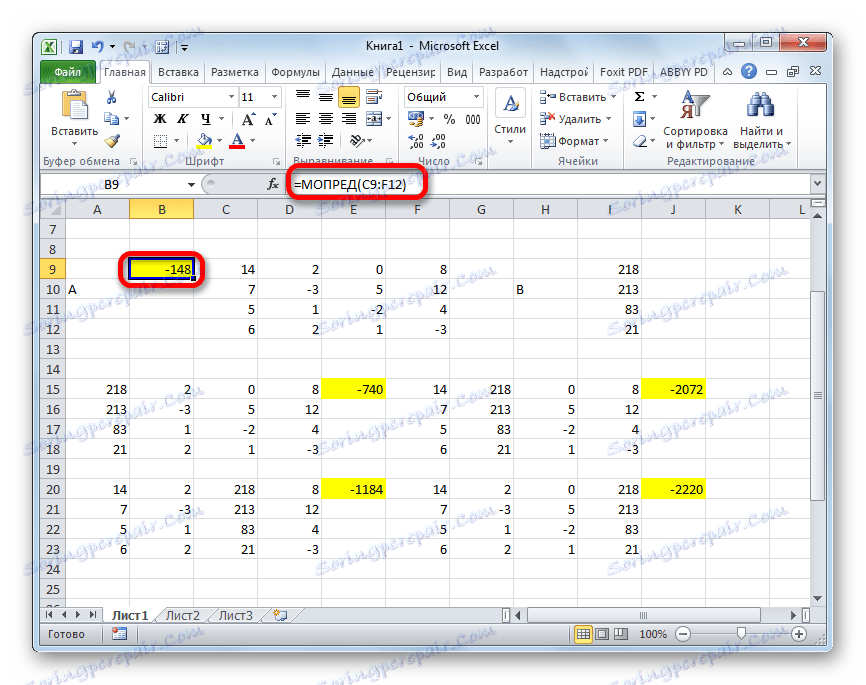
8. На завершальному етапі виробляємо підрахунок визначника первинної матриці. Процедура відбувається все за тим же алгоритмом. Як бачимо, визначник первинної таблиці теж відмінний від нуля, а значить, матриця вважається невироджених, тобто, система рівнянь має рішення.
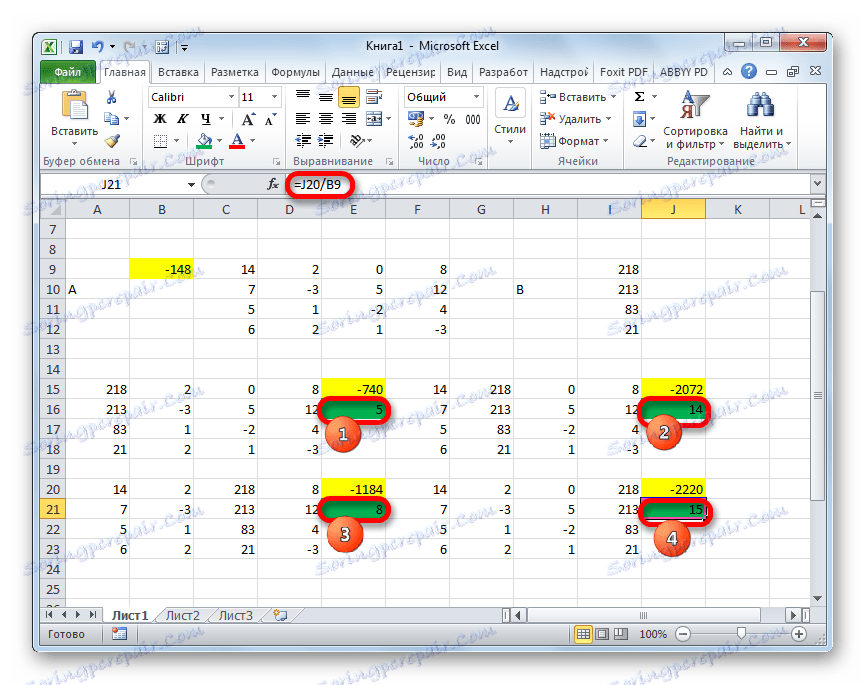
9. Тепер пора знайти корені рівняння. Корінь рівняння дорівнюватиме відношенню визначника відповідної перетвореної матриці на визначник первинної таблиці. Таким чином, розділивши по черзі всі чотири визначника перетворених матриць на число -148, яке є визначником початкової таблиці, ми отримаємо чотири кореня. Як бачимо, вони дорівнюють значенням 5, 14, 8 і 15. Таким чином, вони в точності збігаються з корінням, які ми знайшли, використовуючи зворотний матрицю в способі 1, що підтверджує правильність рішення системи рівнянь.

Спосіб 4: метод Гаусса

Вирішити систему рівнянь можна також, застосувавши метод Гаусса. Для прикладу візьмемо більш просту систему рівнянь з трьох невідомих:


14 x1 +2 x2 +8 x3 =110
7 x1 -3 x2 +5 x3 =32
5 x1 + x2 -2 x3 =17


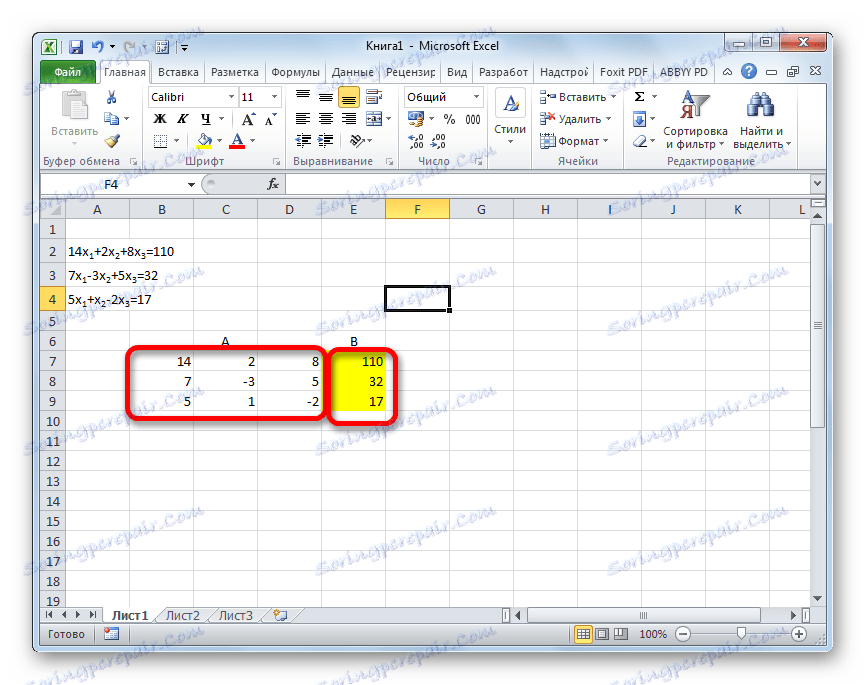
1. Знову послідовно записуємо коефіцієнти в таблицю A, а вільні члени, розташовані після знака «дорівнює» - в таблицю B. Але на цей раз зблизилися обидві таблиці, так як це знадобиться нам для роботи в подальшому. Важливою умовою є те, щоб в першій клітинці матриці A значення було відмінним від нуля. У зворотному випадку слід переставити рядки місцями.
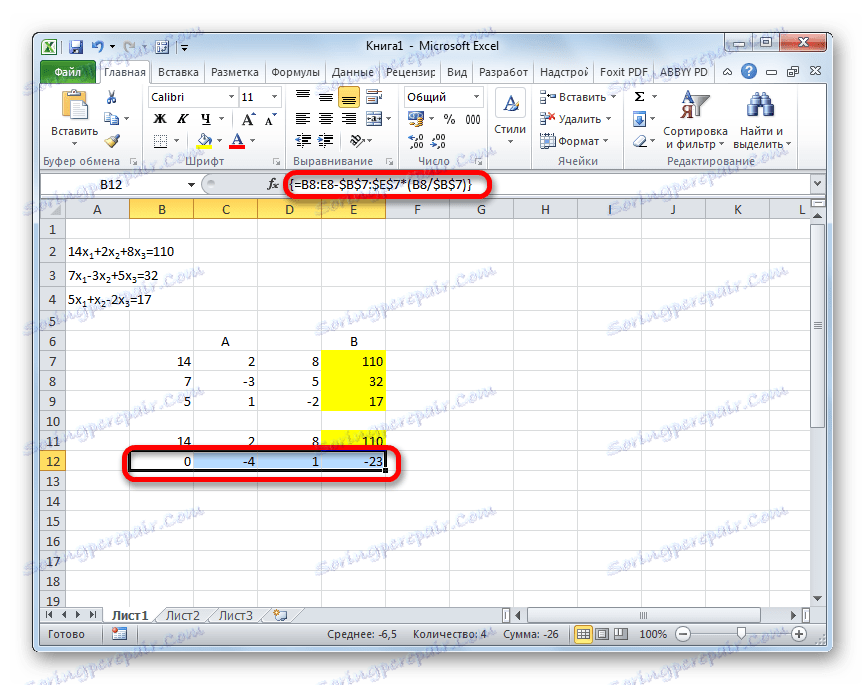
2. Копіюємо перший рядок двох з'єднаних матриць в рядок нижче (для наочності можна пропустити один рядок). У перший осередок, яка розташована в рядку ще нижче попередньої, вводимо наступну формулу:

   =B8:E8-$B$7:$E$7*(B8/$B$7)

   Якщо ви розташували матриці по-іншому, то і адреси осередків формули у вас будуть мати інше значення, але ви зможете вирахувати їх, зіставивши з тими формулами і зображеннями, які наводяться тут.

   Після того, як формула введена, виділіть весь ряд осередків і натисніть комбінацію клавіш Ctrl + Shift + Enter. До ряду буде застосована формула масиву і він буде заповнений значеннями. Таким чином ми зробили віднімання з другого рядка першої, помноженої на відношення перших коефіцієнтів двох перших виразів системи.

3. Після цього копіюємо отриманий рядок і вставляємо її в рядок нижче.
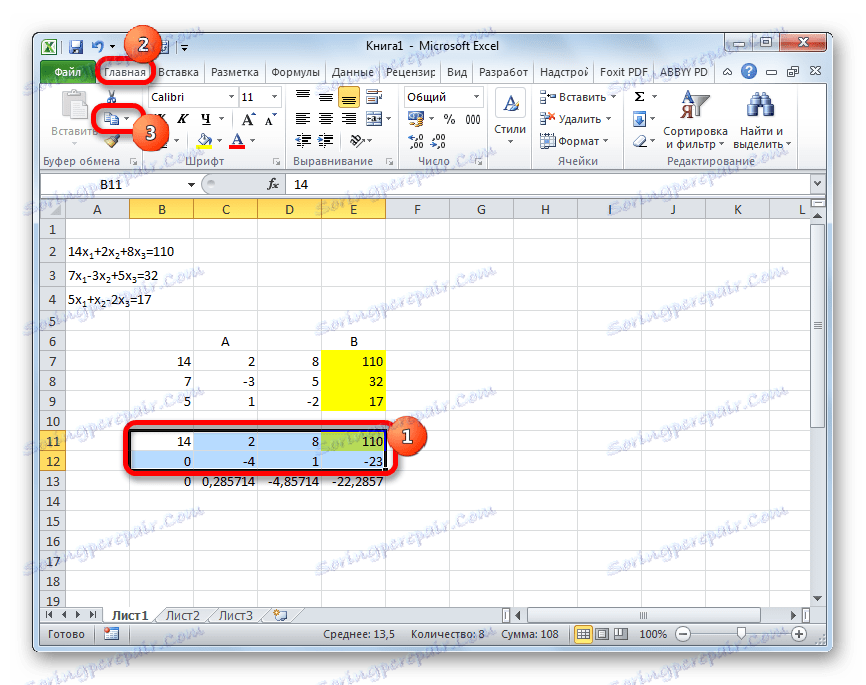
4. Виділяємо два перші рядки після пропущеної рядки. Тиснемо на кнопку «Копіювати», яка розташована на стрічці у вкладці «Головна».
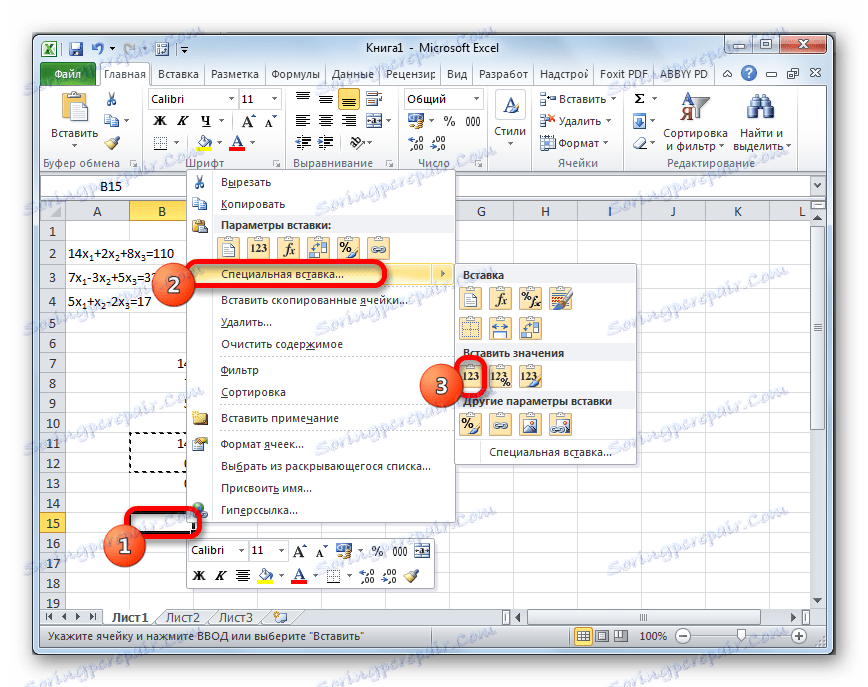
5. Пропускаємо рядок після останнього запису на аркуші. Виділяємо першу осередок в наступному рядку. Натискаємо правою кнопкою миші. У контекстному меню наводимо курсор на пункт «Спеціальна вставка». У запустить додаткові списку вибираємо позицію «Значення».
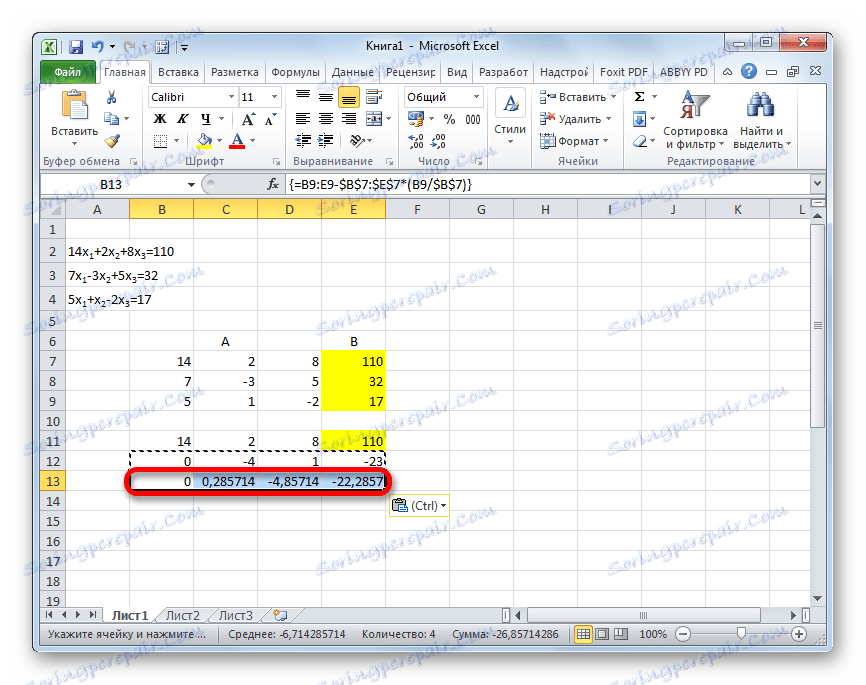
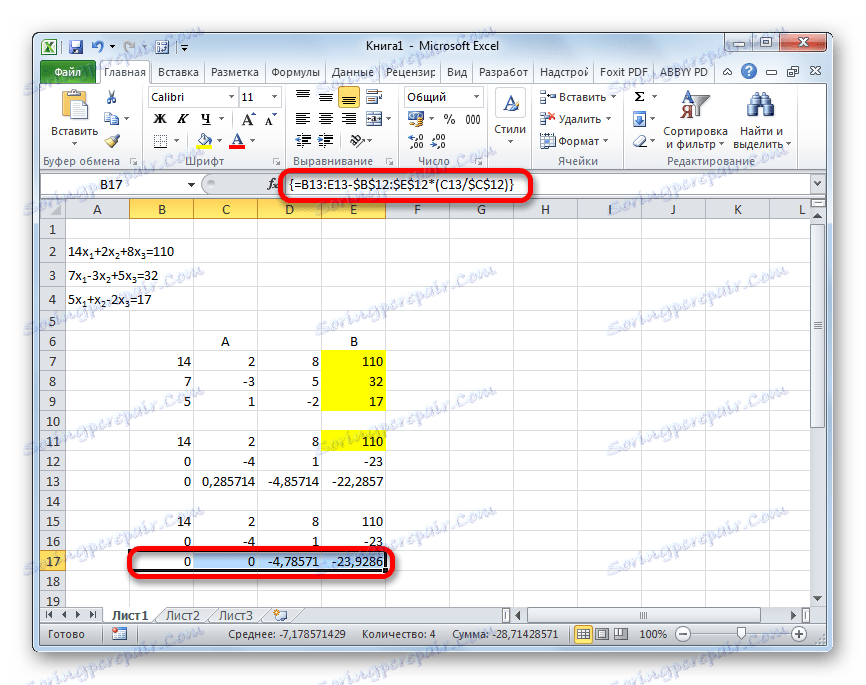
6. У наступний рядок вводимо формулу масиву. У ній виробляється віднімання з третього рядка попередньої групи даних другого рядка, помноженої на відношення другого коефіцієнта третьої і другого рядка. У нашому випадку формула буде мати такий вигляд:

   =B13:E13-$B$12:$E$12*(C13/$C$12)

   Після введення формули виділяємо весь ряд і застосовуємо поєднання клавіш Ctrl + Shift + Enter.

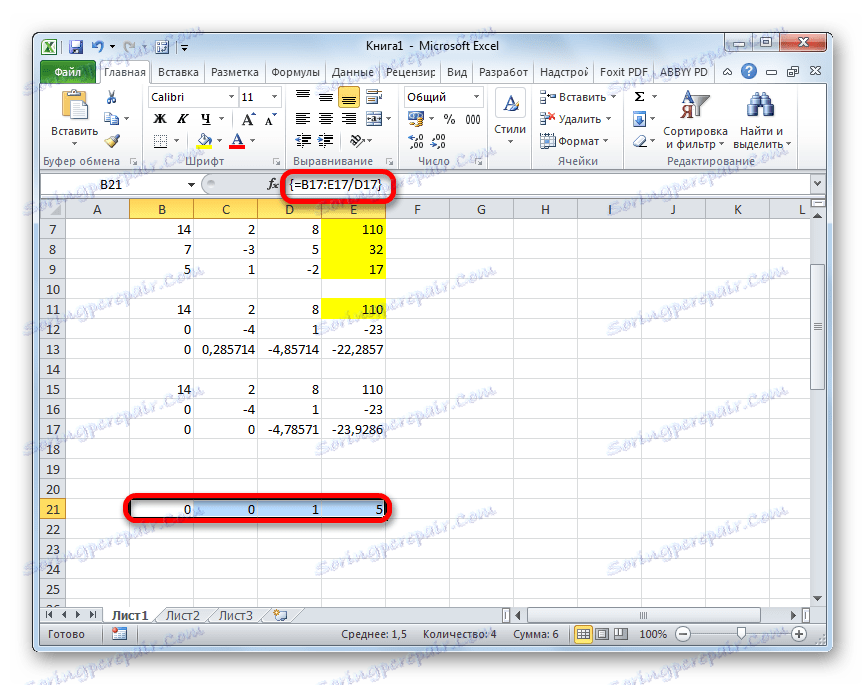
7. Тепер слід виконати зворотну прогонку за методом Гаусса. Пропускаємо три рядки від останнього запису. У четвертому рядку вводимо формулу масиву:

   =B17:E17/D17

   Таким чином, ми ділимо останню розраховану нами рядок на її ж третій коефіцієнт. Після того, як набрали формулу, виділяємо всю строчку і тиснемо поєднання клавіш Ctrl + Shift + Enter.

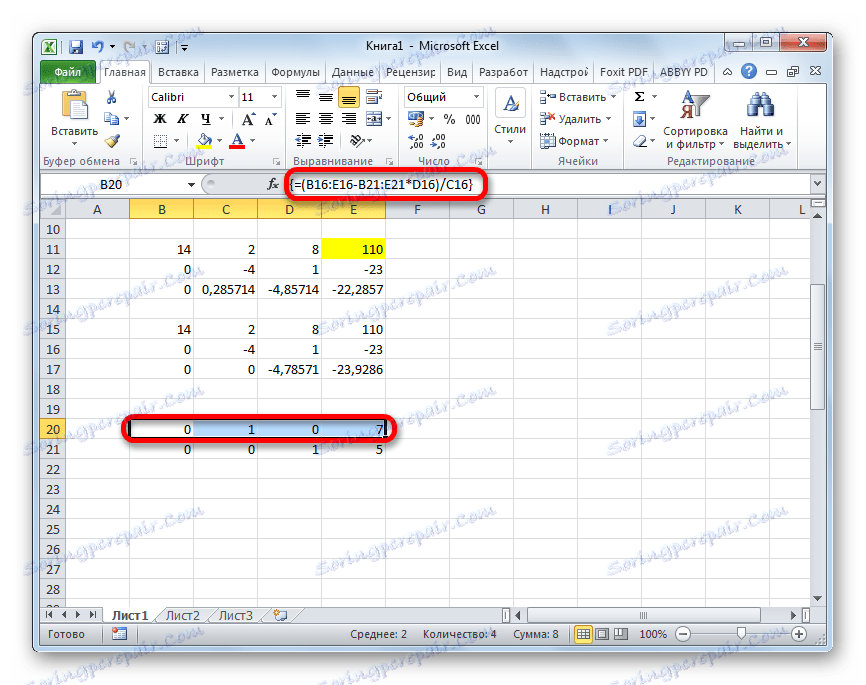
8. Піднімаємося на рядок вгору і вводимо в неї наступну формулу масиву:

   =(B16:E16-B21:E21*D16)/C16

   Тиснемо звичне вже нам поєднання клавіш для застосування формули масиву.

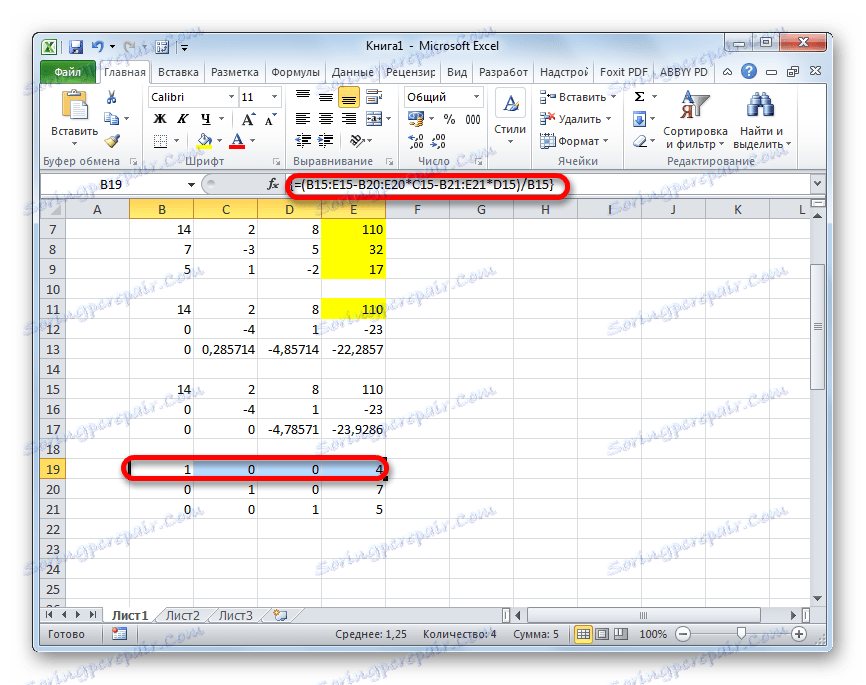
9. Піднімаємося ще на один рядок вище. У неї вводимо формулу масиву такого вигляду:

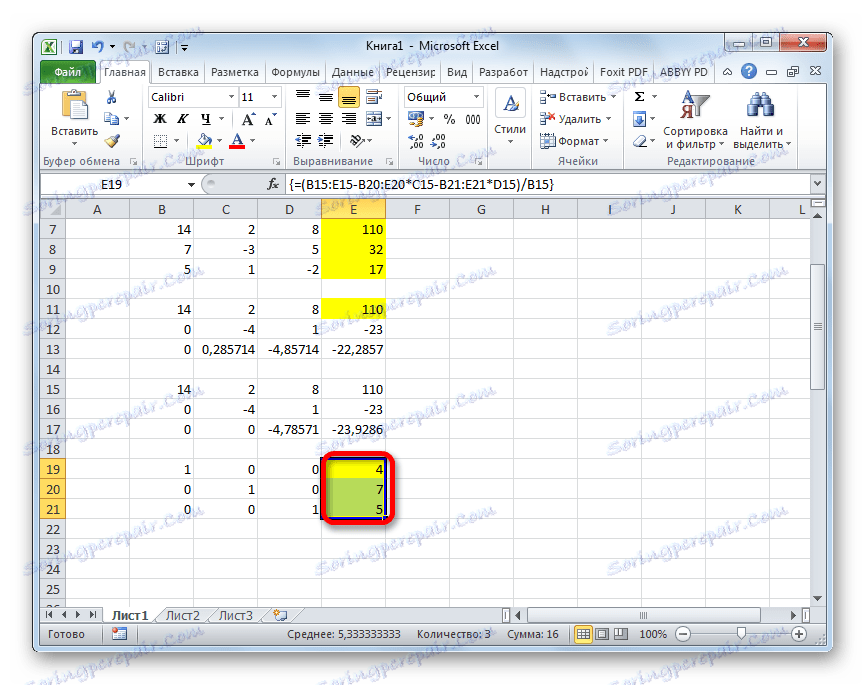
   =(B15:E15-B20:E20*C15-B21:E21*D15)/B15

   Знову виділяємо всю рядок і застосовуємо поєднання клавіш Ctrl + Shift + Enter.

10. Тепер дивимося на числа, які вийшли в останньому стовпці останнього блоку рядків, розрахованого нами раніше. Саме ці числа (4, 7 і 5) будуть корінням даної системи рівнянь. Перевірити це можна, підставивши їх замість значень X1, X2 і X3 в вирази.

Як бачимо, в Ексель систему рівнянь можна вирішити цілу низку способів, кожен з яких має власні переваги і недоліки. Але всі ці методи можна умовно розділити на дві великі групи: матричні і з застосуванням інструменту підбору параметрів. У деяких випадках не завжди матричні методи підходять для вирішення завдання. Зокрема тоді, коли визначник матриці дорівнює нулю. В інших же випадках користувач сам може вирішувати, який варіант він вважає більш зручним для себе.

• ← Побудова параболи в Microsoft Excel
• Створення кнопки в Microsoft Excel →